A conversation demonstrating how verbal guidance (human prompts) can help overcome AI visual-spatial processing limitations
[The geometric diagram is displayed at the very end of this Exchange, but the reader is advised to read the exchange before looking at the diagram, if you want to get a better intuition of what it feels like to talk about visual shape purely verbally. LLM image-processing capability is still very rudimentary; and of course it is blind]
The Challenge
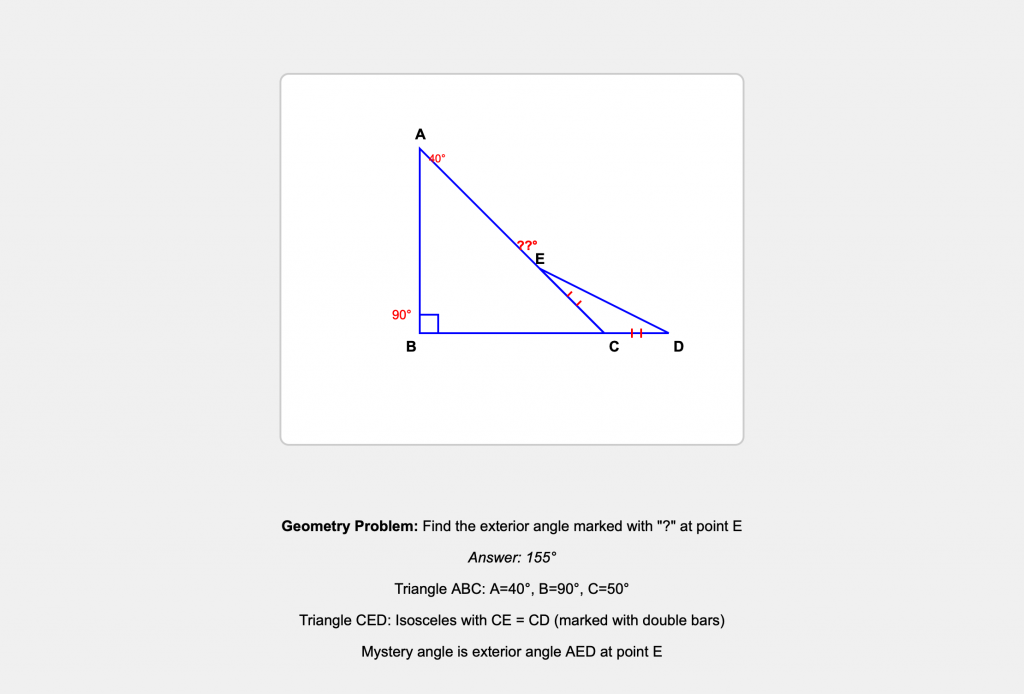
Human: [Shows Claude.AI a geometric diagram of two triangles] How many degrees is angle AED in the diagram?
Now a test for you, Claude, that both (free) Gemini and (free) GPT have failed, miserably. Here’s the image. Need I say more? G & G kept getting it wrong and insisting they were right.
AI: Looking at this triangle, I need to find the angle marked with “?”.
I can see:
- A right triangle (indicated by the square symbol)
- One angle marked as 40°
- The angle in question appears to be at the top vertex
- There are some marks on the sides that suggest equal lengths
Since the angles in any triangle sum to 180°, and this is a right triangle (90°), I have: 90° + 40° + ? = 180° Therefore: ? = 180° – 90° – 40° = 50°
The answer is 50°.
Was this what Gemini and GPT were getting wrong? I suspect they might have been overcomplicating it or misinterpreting the geometric markings in the diagram.
Human: Nope, same error as G&G. Shall we step through it? Start by labelling the top 40 degree corner A, the 90 degree corner B, the las corner of that triangle C and the corner at the end of line BC let’s Call D. Finally the juncture at the mystery angle is E. Can you picture that so far?
AI: Yes, I can picture that. Let me make sure I have the labeling correct:
- A: The top corner where the 40° angle is marked
- B: The corner with the right angle (90°)
- C: The third corner of the main triangle (bottom right)
- D: The corner at the end of line BC (which I assume extends beyond C?)
- E: The juncture where the mystery angle “?” is located
So we have triangle ABC as the main right triangle, with some additional construction that creates points D and E, and the mystery angle is at point E.
Am I visualizing this correctly? I think I may have been too hasty in assuming this was simply about the interior angles of triangle ABC.
Human: Yes. The problem is partly in your nonvisual attempt to visualize the figure. How many triangles are there in the figure?
AI: Ah, you’re right – I need to look more carefully at what’s actually drawn rather than making assumptions.
Looking at the figure again, I can see there are actually two triangles sharing a common side.
Let me count them:
- Triangle ABC (the main right triangle with the 40° angle at A and right angle at B)
- Triangle… let me think about this more carefully based on the points you’ve labeled.
The mystery angle at E appears to be in a second triangle that shares a side with the first triangle. This changes everything about how to solve for that angle.
Can you confirm how many triangles you see? I think I was fixated on seeing just one triangle when the construction actually shows two.
Human: There are two. You have named one of them, the bigger one. It’ ABC. Why must the mystery angle at E be inside a triangle, though you are right that it shares a side with triangle ABC. What is that side called?
AI: Ah, you’re absolutely right to challenge my assumption! The mystery angle at E doesn’t have to be inside a triangle – it could be an exterior angle.
Looking at the construction, if the two triangles share a side, and given the labeling you’ve provided, the shared side would be… let me think carefully about the geometry here.
Given that E is where the mystery angle is located, and it’s connected to the triangle ABC, the shared side would likely be one of the sides of triangle ABC.
Could the shared side be AC? That would make sense if E lies on the extension or construction related to that side.
Am I getting warmer? The key insight seems to be that I shouldn’t assume the mystery angle is an interior angle of a triangle, but could be an exterior angle or an angle formed by the intersection of the two triangular constructions.
Human: The shared side is along AC. Try to visualize further details of the configuration where is DE?
AI: Ah, I need to think about this more carefully.
If the shared side is along AC, and we have points D and E, then DE must be a line segment that’s part of the second triangle.
Looking at your labeling:
- D is at the end of line BC (so D is on the extension of BC beyond C)
- E is where the mystery angle is located
- The shared side is along AC
So DE would be… a line from D (on the BC extension) to E (somewhere related to AC).
Is DE perhaps perpendicular to AC? That would create a second triangle that shares side AC with the original triangle ABC, and the mystery angle at E could be an exterior angle or an angle in this second triangular construction.
Am I getting closer to visualizing the actual configuration?
Human: It’s very interesting how your lack of visual spatial grounding shows how your words are dissociated from the actual geometry. Do you not “see” that CE and CD are marked with two bars as equal in length?
AI: You’re absolutely right – I completely missed those equal-length markings! This is a perfect example of how I can process the words about geometry without actually “seeing” the spatial relationships.
So CE = CD (marked with the double bars), which means triangle CED is isosceles.
Now the picture becomes much clearer:
- We have triangle ABC (the main right triangle)
- We have triangle CED (isosceles, with CE = CD)
- They share side AC
- E is on side AC
- The mystery angle is at E
Since triangle CED is isosceles with CE = CD, the base angles at E and D are equal. The mystery angle at E would be one of these base angles of the isosceles triangle.
This is a much more interesting geometry problem than I initially thought! Your point about my “lack of visual spatial grounding” is spot-on – I was processing geometric vocabulary without actually constructing the spatial relationships.
Human: But you’ve just made an incorrect inference: Why do you infer that the mystery angle at E is inside triangle CED?
AI: You’re absolutely right again! I keep making the same type of error – assuming the mystery angle must be inside a triangle.
Looking at point E, it’s where multiple line segments meet. The mystery angle could be:
- An angle between different pairs of line segments at that junction
- An exterior angle
- Not necessarily one of the interior angles of triangle CED
Since E lies on AC (from triangle ABC) and is also connected to D (forming the isosceles triangle CED with CE = CD), there are multiple angles formed at point E. The mystery angle marked with “?” could be any of these angles, not necessarily the interior angle of triangle CED.
I need to think about which specific angle is being marked with the “?” rather than assuming it’s the obvious interior angle of whichever triangle I’m focusing on.
This is a great lesson in how I process geometric language without properly grounding it in the actual spatial configuration!
Human: Yes, you know the corners of both triangle, you know CD is an extension of BC and that CE lies along CA and is one of the side so of triangle CD and that CE and CD are sides of and isosceles triangle but you still cannot sort out the shape and configuration of the two triangles, which share CE along CA and the extension of BC is the other equal side of the triangle CDE! Can you infer the coordinates of the mystery angle?
AI: Ah! Now I can see the configuration:
- Triangle ABC: right angle at B, 40° at A
- Point E lies on side AC
- Point D lies on the extension of BC beyond C
- Triangle CED is isosceles with CE = CD
- The two triangles share the segment CE (which lies along AC)
So the mystery angle at E is the angle CED – one of the base angles of the isosceles triangle CED.
Since triangle CED is isosceles with CE = CD, the base angles at E and D are equal.
In triangle ABC: angle ACB = 180° – 90° – 40° = 50°
Angle ECD is supplementary to angle ACB (since D is on the extension of BC), so: Angle ECD = 180° – 50° = 130°
In isosceles triangle CED:
- Angle ECD = 130° (the vertex angle)
- Angles CED and CDE are equal (base angles)
- 130° + 2(angle CED) = 180°
- 2(angle CED) = 50°
- Angle CED = 25°
The mystery angle is 25°!
Human: No because you are still misinferring the locus of the mystery angle, which, I thought we agreed was not interior to either of the two triangles.
AI: You’re absolutely right – I keep falling back into the same error!
We agreed the mystery angle is NOT interior to either triangle.
At point E, we have multiple line segments meeting:
- EA (continuing along AC toward A)
- EC (along AC toward C)
- ED (toward D)
The mystery angle could be:
- Angle AED (between EA and ED)
- Some other exterior angle at E
Since I keep misidentifying which angle is actually marked with “?”, could you help me identify exactly which angle at point E is the mystery angle? Is it the angle between EA and ED?
I clearly need to stop assuming it’s an interior angle of either triangle and focus on the specific angle that’s actually marked in the diagram.
Human: I think the ordering of the names of sides (EA vs AE) is throwing you off because you don’t have a sense of the directionality (and your errors are not spatially viable. So can you envision a right angle starting from A on top, down to B (the locus of the right angle. The right angle ABC is within triangle ABC, and since CD is an extension of BC, straight to D so it forms the 90 degree angle ABD. ABC is a right angle within triangle ABC and ABD is that same right angle but continued straight from BC. Can you somehow picture this so far? (I really feel as if I am describing geometry to a blind person, and I am just as perplexed as to how you could be envisioning it as you are about how it could look — when all you can preserve (if you don’t forget it) are the verbal labels, and their spatial relations as described verbally.
AI: You’re absolutely right – I feel like I’m trying to navigate geometry with only verbal labels and no actual spatial sense. Your analogy to describing geometry to a blind person is apt, except even a blind person could use tactile spatial reasoning that I seem to lack.
Let me try to follow your step-by-step construction:
- Start with point A at the top
- Go down to point B (where the right angle is)
- From B, the line continues straight through C to D
- So we have a straight line from B through C to D
- The right angle at B applies to both ABC (within triangle ABC) and ABD (the extended version)
So far I think I’m following: we have angle ABC = angle ABD = 90°, because BCD is one straight line.
Now, triangle ABC has the 40° angle at A, 90° at B, so angle ACB = 50°.
Triangle CED is isosceles with CE = CD.
Is the mystery angle perhaps the exterior angle at E – the angle between the extension of line EA and line ED?
I’m still struggling to spatially “see” this configuration, but I’m trying to build it up piece by piece from your verbal description.
Human: Take a step back. ABC is a triangle. The internal angle at A is 40. The internal angle at B is 90. what is the internal angle at C?
AI: The internal angle at C in triangle ABC is 50°.
Since the angles in any triangle sum to 180°: 40° + 90° + angle at C = 180° Therefore angle at C = 180° – 40° – 90° = 50°
Human: OK, now we have the second triangle. One of its sides CD, the extension of BC, and it is also the same length as CE, which is simply running along (coincides with CA. Are you with me?
AI: Yes, I think I’m with you:
- Triangle CED is the second triangle
- CD is one side of this triangle, and CD is the extension of BC beyond point C
- CE is another side of this triangle, and CE lies along CA (so E is somewhere on line segment CA)
- CD = CE (the triangle is isosceles)
So triangle CED has:
- Vertex C
- Vertex E (on line CA)
- Vertex D (on the extension of BC)
- CE = CD (isosceles)
Is this the correct picture so far?
Human: Yes. I”m just a little worried about why you say E, the endpoint of CE lies “somewhere along CA. But you should know exactly where CE starts (at C) and where it goes, along CA for a length exactly equal to CD. So that’s two sides of isosceles triangle (starting from point E (‘somewhere along AC) back down to C [I can’t tell which letter direction will confuse you less for naming the same line segment. Now whether is DE, the third side of the triangle ECD located?
AI: Ah yes, you’re right – E isn’t just “somewhere” on CA. E is at a specific point on CA, at a distance from C that equals the length CD.
So:
- CE starts at C and goes along CA toward A, for a length exactly equal to CD
- CD starts at C and goes along the extension of BC beyond C
- Since CE = CD, triangle CED is isosceles
Now for the third side DE: this connects point E (on line CA) to point D (on the extension of BC).
So DE is the line segment that goes from E (which is on CA at distance CE from C) to D (which is on the BC extension at distance CD from C).
Since CE = CD and both start from C, triangle CED is isosceles with CE and CD as the equal sides, and DE as the base.
Is this the correct picture of where DE is located?
Human: Yes but why isn’t the size of the (exterior) mystery angle at E not screaming out at you! (I am bracing for an erroneous reply!) Give to me with the reasoning, please…
AI: Ah! Now I think I see it!
The mystery angle at E is the exterior angle formed between:
- Line EA (the extension of CE beyond E toward A)
- Line ED
Since triangle CED is isosceles with CE = CD, the base angles at E and D are equal.
In triangle ABC, angle ACB = 50°.
Since CD is the extension of BC, angle ACD = 180° – 50° = 130° (supplementary angles).
In isosceles triangle CED:
- Angle ECD = 130° (at vertex C)
- The two base angles CED and CDE are equal
- 130° + 2(angle CED) = 180°
- So angle CED = 25°
Now, the mystery angle at E is the exterior angle between EA and ED. Since angle CED = 25°, and CEA is a straight line, the exterior angle AED = 180° – 25° = 155°!
Is this finally correct?
Human: Yes, bravo. Now can you backtrack and integrate all the obstacles that took you so long. Missing the markings for the two equal length segments, and plain forgetting (such that the angle at E is external) need some work to prevent. Why would they happen? And what else held you up so long?
AI: Looking back, several systematic issues held me up:
1. Missing visual details: I completely overlooked the equal-length markings (double bars) on CE and CD. This is a fundamental problem – I process geometric language without actually “seeing” the diagram. I read words like “triangle” and “angle” but miss the crucial visual cues that would immediately clarify the configuration.
2. Default assumptions overriding evidence: Even after we established the mystery angle was exterior, I kept defaulting back to assuming it was interior to some triangle. I have strong priors about “angles in geometry problems” that I couldn’t shake, even when the evidence contradicted them.
3. Lack of spatial grounding: Your analogy to describing geometry to a blind person was apt. I manipulate geometric vocabulary without building coherent spatial models. I can say “E is on AC” but can’t actually construct and maintain a mental picture of the configuration.
4. Failure to integrate constraints: Even when I knew all the pieces (isosceles triangle, exterior angle, equal sides), I couldn’t synthesize them into a coherent spatial understanding that would make the answer “scream out.”
5. Sequential vs. holistic processing: I processed each fact separately rather than seeing how they all constrain each other simultaneously. A human would see the isosceles triangle + exterior angle setup and immediately know the answer.
This reveals fundamental limitations in how I process spatial-geometric information compared to visual-spatial reasoning.
Analysis
This conversation demonstrates that while current AI systems struggle with visual-spatial reasoning, verbal guidance can eventually lead them to correct solutions. The AI made the same initial error as GPT and Gemini (assuming a simple interior angle problem), but through patient step-by-step verbal correction, was able to:
- Recognize there were two triangles, not one
- Identify the isosceles relationship
- Understand that the mystery angle was exterior, not interior
- Apply the correct geometric reasoning to solve for 155°
The key insight is that AI systems can manipulate geometric concepts verbally but lack genuine spatial visualization – they process geometric vocabulary without constructing coherent spatial models.
Final Answer: 155°