Depuis le début du XXe siècle, une question apparemment technique a joué un rôle fondateur bien au-delà de la logique et des mathématiques : qu’est-ce que de « calculer » ? Lorsque nous disons qu’un mathématicien calcule, que fait‑il exactement ? Quelles opérations sont légitimes, lesquelles ne le sont pas, et comment les caractériser sans faire appel à l’intuition vague du « bon raisonnement » ou de l’ingéniosité humaine ? C’est ce problème précis qui a mobilisé, dans les années 1930, plusieurs logiciens – Church, Turing, Post, Kleene, Gödel – et qui a conduit à une clarification conceptuelle dont les retombées structurent encore aujourd’hui les sciences cognitives.
Il est essentiel de rappeler que le but initial n’était pas de construire des ordinateurs, ni d’expliquer l’esprit humain, mais de formaliser ce que font effectivement les mathématiciens lorsqu’ils effectuent un calcul rigoureux. Il s’agissait de cerner la notion de « procédure effective » : une suite d’étapes finies, explicites, mécaniquement applicables, qui transforment des symboles initiaux en symboles finaux. Autrement dit, il fallait rendre explicite ce qui, jusque‑là, était implicitement confié à l’intelligence humaine.
Ce qui est frappant rétrospectivement, c’est que ces auteurs ont proposé des modèles très différents en apparence. Church a introduit le λ‑calcul, Gödel des fonctions récursives, Post des systèmes de production, Kleene des schémas formels, et Turing sa célèbre machine abstraite « la machine de Turing ». Pourtant, malgré leurs différences de présentation, tous ces modèles se sont révélés complètement équivalents : tout ce qui est calculable dans l’un l’est aussi dans les autres. Cette convergence inattendue a donné un poids considérable à l’idée qu’ils avaient tous, chacun à sa manière, capturé la même notion fondamentale : la computation.
Parmi ces modèles, la machine de Turing s’est imposée non parce qu’elle serait plus puissante, mais parce qu’elle est conceptuellement la plus simple et la plus parlante. Elle permet de voir, presque physiquement, ce qu’est une computation. Une machine de Turing se compose d’un ruban potentiellement infini, divisé en cases, sur lesquelles sont inscrits des symboles discrets pris dans un alphabet fini. Une tête de lecture‑écriture parcourt ce ruban, une case à la fois. À chaque étape, la machine se trouve dans un état interne déterminé, parmi un ensemble fini d’états possibles.
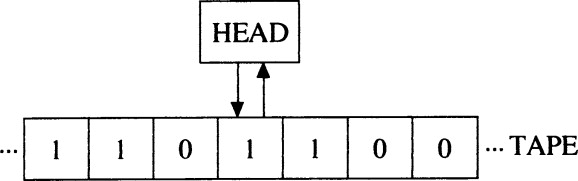
Le fonctionnement est entièrement régi par une table de règles. Chaque règle dit : si la machine est dans tel état interne et si le symbole actuellement lu sur le ruban a telle forme, alors il faut accomplir exactement trois choses : éventuellement remplacer ce symbole par un autre, déplacer la tête d’une case vers la gauche ou vers la droite, et passer dans un nouvel état interne. Rien de plus. Il n’y a ni compréhension, ni interprétation, ni « prise de décision » au sens psychologique. Tout est déterminé par la forme du symbole et par l’état courant de la machine. Et ceci est ce que veut dire « la manipulation des symboles » .
La computation est:
la manipulation des symboles:
suivant des règles (algorithmes)
qui ne portent que sur la forme (arbitraire) des symboles
(pas sur leur sens)
et qui sont independents du matériel mais….
interprétable sémantiquement (par l’utilisateur)
Il est crucial d’insister sur la forme arbitraire des symboles. Les symboles manipulés par une machine de Turing n’ont aucune signification « intrinsèque ». Ils peuvent être des 0 et des 1, des lettres, des traits, ou n’importe quelle autre marque distincte. Ce qui compte, ce n’est pas ce qu’ils représentent éventuellement pour un observateur humain, mais uniquement leurs différences de forme, car ce sont ces différences qui déclenchent les règles de transition (manipulation). La computation est donc, par définition, une manipulation syntaxique (formelle) : elle opère sur des formes, non sur des significations.
Les règles elles‑mêmes sont ce qu’on appelle des algorithmes. Un algorithme est une procédure formelle, finiment spécifiée, qui détermine sans ambiguïté quelles opérations doivent être effectuées à chaque étape. Un point fondamental, souvent mal compris, est que l’algorithme ne « sait » pas ce qu’il fait. Il ne calcule pas parce qu’il vise un résultat ou comprend un problème, mais parce que ses règles sont suivies mécaniquement. Le fait que le résultat puisse ensuite être interprété comme la solution d’une équation ou la réponse à une question est entièrement externe à la computation elle‑même.
Cette distinction conduit à une autre propriété centrale de la computation : son indépendance par rapport à l’implémentation matérielle. Une même machine de Turing abstraite peut être réalisée de multiples façons physiques : avec des engrenages, des relais électromécaniques, des circuits électroniques, ou même, en principe, avec du papier et un crayon, pourvu qu’un humain suive les règles à la lettre. Tant que la même suite d’états et de manipulations symboliques est respectée, c’est exactement la même computation qui est effectuée. Les différences matérielles n’affectent pas la nature du calcul, seulement sa vitesse, sa fiabilité ou son coût.
Cette indépendance est décisive pour les sciences cognitives, car elle implique que la computation, en tant que telle, est définie au niveau formel, non au niveau physique. Le matériel réalise l’algorithme, mais ne le définit pas. Inversement, l’algorithme n’inclut aucune référence à ce que le matériel est ou à ce qu’il représente. Il n’y a là aucune place pour la sémantique, sauf comme interprétation ajoutée par un observateur externe.
C’est dans ce contexte qu’il faut comprendre la thèse dite de Church‑Turing, dans sa version « faible ». Elle affirme que tout ce qu’un mathématicien humain peut calculer par une procédure effective peut, en principe, être calculé par une machine de Turing. Il ne s’agit pas d’une hypthèse empirique au sens habituel, ni d’un théorème formel qu’on peut démontrer mathématiquement, mais d’une thèse conceptuelle : une conjecture qu’on peut falsifier, mais pas proouver vraie. Elle repose sur l’argument que les différentes tentatives de formalisation du calcul effectif convergent toutes vers la même classe de fonctions calculables, et que jusqu’à présent, aucune contre‑exemple convaincant n’a été proposé.
Il est important de ne pas surinterpréter cette thèse. Elle ne dit pas que tout ce qui existe est calculable, ni que l’esprit humain se réduit à une machine de Turing. Elle dit quelque chose de beaucoup plus précis et plus modeste : si une activité mérite le nom de calcul effectif, alors elle est Turing‑calculable. Cette précision sera essentielle lorsque nous aborderons, plus tard dans le cours, les questions de cognition, de langage et de compréhension.
On parle parfois d’une version « forte » de la thèse de Church‑Turing, selon laquelle presque tout processus physique peut être simulé par une machine de Turing avec une précision arbitraire. Cette idée est largement acceptée dans les sciences physiques contemporaines, mais elle est souvent mal comprise. Simuler un phénomène n’est pas le réaliser. Une simulation numérique d’un ouragan ne mouille personne, et une simulation de digestion ne produit aucune calorie. De la même façon, une simulation informatique d’un cœur ne pompe pas de sang.
L’analogie avec « l’impression 3D » est éclairante. Un programme peut décrire formellement la structure d’un objet ; cette description peut être utilisée pour en simuler le comportement, par exemple dans un environnement virtuel. Mais pour produire l’objet réel, il faut un dispositif physique supplémentaire, capable de transformer la description en matière. La computation fournit la description et la simulation, non la réalisation matérielle. Confondre les deux conduit à des erreurs conceptuelles profondes.
Ces distinctions – entre syntaxe et sémantique, entre algorithme et interprétation, entre simulation et réalité – ne sont pas de simples subtilités philosophiques. Elles constituent l’armature conceptuelle qui permettra, dans les semaines à venir, de poser correctement les questions sur la cognition, le langage, le test de Turing, l’argument de la pièce chinoise, et le problème de l’ancrage symbolique. Avant de se demander si la cognition est computationnelle, ou si une machine peut comprendre, il faut d’abord savoir, avec précision, ce que la computation est, et ce qu’elle n’est pas.
Et qu’est-ce qui est une « machine » ? Il faut aussi dissiper une autre confusion, plus générale encore, qui revient sans cesse dans les discussions sur l’esprit, la cognition et l’intelligence artificielle. On entend souvent des déclarations du genre : « Ça, c’est quelque chose qu’une machine ne pourra jamais faire. » Mais, prise littéralement, cette phrase est presque toujours vide. Tout système dynamique qui évolue conformément aux lois de la causalité est, en ce sens minimal et non métaphorique, une machine — un mécanisme. Qu’il soit conçu par des humains ou qu’il se trouve tel quel dans la nature n’y change rien. Une horloge, une automobile, un ordinateur, un robot, une imprimante 3D, un système autonome, un cerveau humain, un organisme biologique, une colonie de bactéries, un système planétaire ou une constellation stellaire sont tous des systèmes causaux : à un état donné succède un autre état, selon des régularités déterminées par leur structure et par les lois physiques. Dire qu’un humain n’est « pas une machine » mais qu’un ordinateur en est une, ce n’est pas une thèse scientifique ; c’est une façon de parler. La vraie question n’est jamais de savoir si quelque chose est ou n’est pas une machine, mais de quel type de mécanisme il s’agit, et de quelles capacités ce mécanisme peut ou ne peut pas générer. Si une capacité est causale — si elle consiste à faire quelque chose dans le monde — alors, par définition, elle doit être produite par un mécanisme. Affirmer qu’« une machine » ne pourrait jamais faire X revient donc soit à une hypothèse empirique précise (à discuter), soit à une erreur conceptuelle. En cas de doute, il vaut mieux suspendre l’affirmation et examiner de quel mécanisme on parle réellement.
