Measuring Height
This learning object extends the parameters of aerial photographs which have already been covered, to introduce the concept of making quantitative measurements of the heights of objects on the ground from aerial photos.
Relief displacement
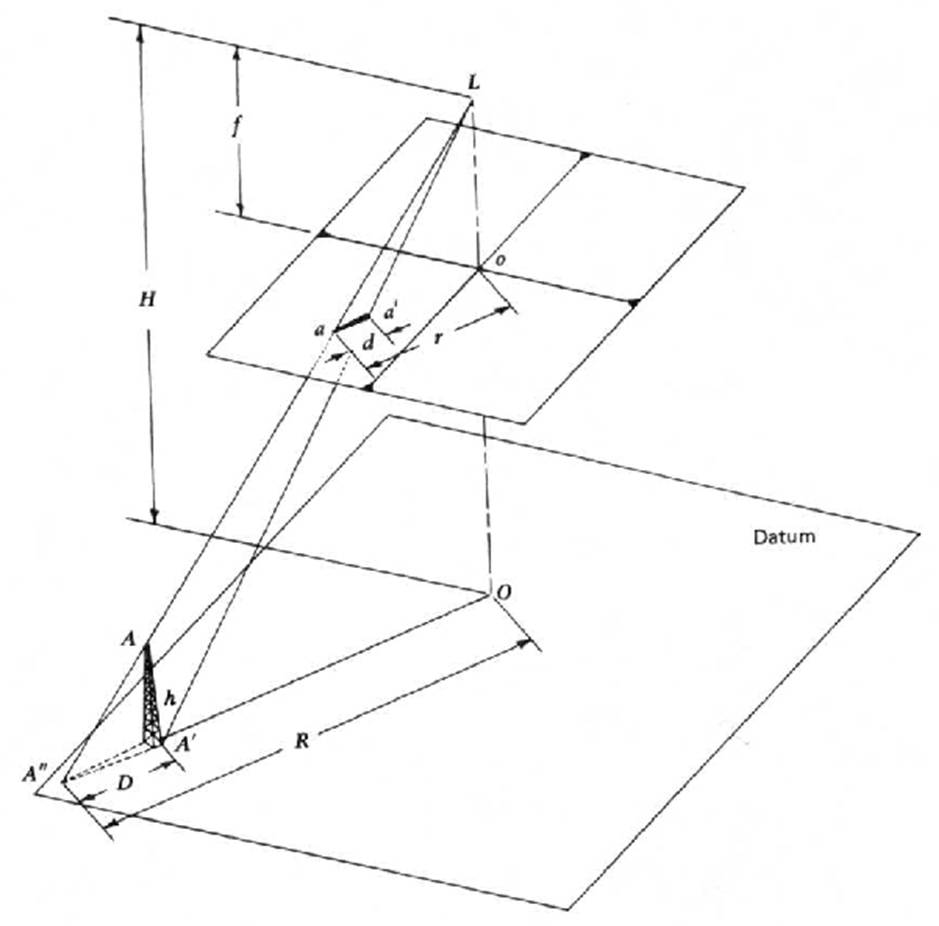
Due to the central perspective projection of the camera system, tall objects on the ground appear to be displaced outwards from the centre of the photo. Such a displacement is called relief (i.e. height) displacement. In order to measure the relief displacement, we need to measure the distance from the centre of the photo to the base (say ‘b’) of the object and to its top (say ‘t’). The amount of displacement (t-b) can be used to measure the height of the object. The following animation explains the process of measuring relief displacement in a photograph. The first step is to identify the principal point which is normally identified by connecting all the fiducial marks.
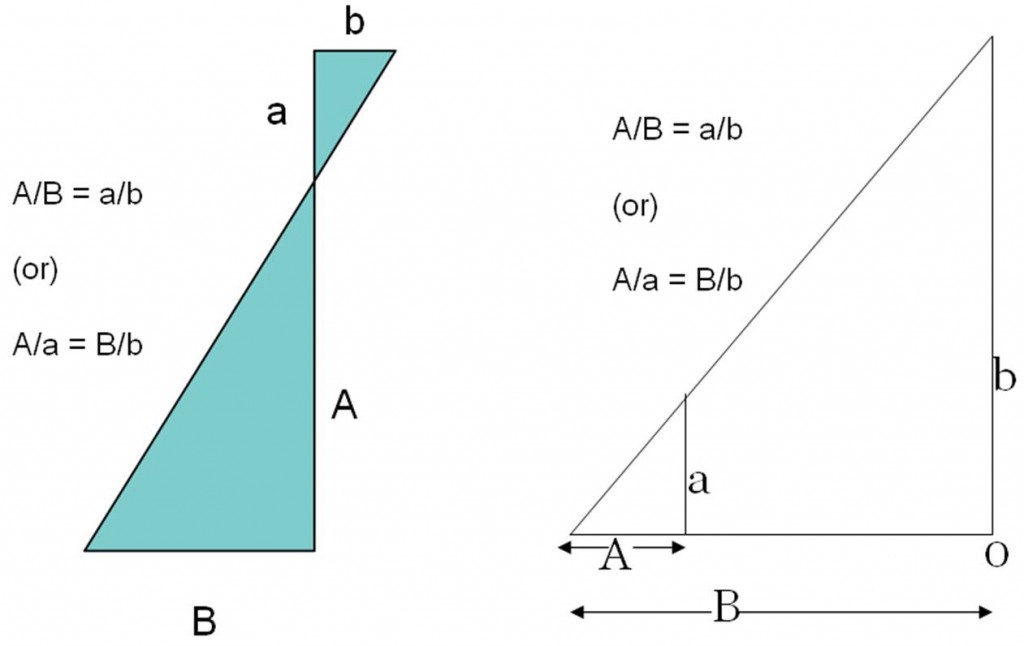
If the terrain in the study area has a lot of undulations then we will have varying amounts of relief displacement, and hence the scale will be different at different locations and not constant across the aerial photograph. The magnitude of relief displacement depends on the geometric relationships between flying height, the radial distance from the principal point (radial position, r) and the height of the object on the ground. From this relationship we can calculate the height of objects on the ground. The law of similar triangles plays an important role in all photogrammetric calculations and the following pictures gives examples of the law of similar triangles (if two triangles are similar and one is an enlarged or scaled version of the other then we can apply the law of similar triangles).
The geometric relationship between the ground and corresponding image objects have been intelligently integrated for measurimg the height of an object using the relief displacement. The animation below explains the steps involved in measuring the height of an object from an aerial photo measurement, using simple 2D triangles.
Reflection
Using the concepts explained above, estimate the height of a tower using the measurements given below:
If the radial displacement of a tower on an aerial photograph is 3 mm and the radial distance from the principal point to the top of the tower is 50 mm, and the flying height is 1200 m above the base of the tower, what is the actual height of the tower on the ground?
h = (t-b) H / t = relief displacement x flying height / radial distance
(3 mm x 1200 m) / 50 mm = 72 m
Reflection
Can you work out how to calculate the relief displacement (d) (in terms of an equation using the law of similar triangles) from the following image? Click on the button below to see an animated explanation.
Click to advance the slides in this animation for an explanation of the calculation:
Reading Activity
Explore the website http://www.globalmapping.uk.com/index.asp provided by Ordnance Survey, UK. Find out what OS is doing in terms of aerial photography and photogrammetric applications.
For further recommended reading, see:
Lillesand, T. M., Kiefer, R. W. and Chipman, J. W. 2008 Remote Sensing and Image Interpretation, John Wiley & Sons, New Jersey.