INTRODUCTION & BRIEF HISTORY
At the self-proclaimed “heart” of Google’s software (2014) lies their remarkable PageRank algorithm. PageRank added an extra hypertextual layer of abstraction to earlier keyword driven search models used by companies such as AltaVista and Infoseek (Chater & Oaksford, 2008). PageRank utilised a weighted ranking algorithm that took into account the number of hyperlinks pointing towards a connected page and their interrelation with other popular websites (Brin & Page, 1998). Named after its inventor Google founder Larry Page (not just a simple reference to the “pages” being ranked) (Page, 2001) PageRank was based upon previous conceptual ideas of academic citation using hypertext technology. These original principles were pioneered through the earlier works of Ellen Spertus (1997) and Massimo Marchiori (1997). These early concepts around hypertext and academic citation where then modified and applied directly to ranking webpages popularity and their relevance to web user’s search queries.
ALGORITHM BREAKDOWN
The PageRank Algorithm uses a probabilistic distribution to calculate the rank of a website. This rank is then updated every time Google’s web-crawler scours the web. This follows the Random Surfer Model which models user behaviour based on the probability that they will follow a hyperlink to a new site or randomly leave and request a new page.
There have been two public versions of the PageRank algorithm released which were famously mixed up by the Google founder Serge Brin and Larry Page in their original paper The Anatomy of a Large-Scale Hypertextual Web Search Engine (1998).
Figure 1. PageRank without the damping factor being relative to the number of pages
PR(A) = (1-d) + d (PR(W1)/C(W1) + … + PR(Wn)/C(Wn))
Figure 2. PageRank with the damping factor relative to the number of pages
PR(A) = (1-d) / N + d (PR(T1)/C(T1) + … + PR(Tn)/C(Tn))
ALGORITHM KEY FOR FIGURE 1: from http://interestingwebs.blogspot.co.uk/2009/05/simple-explain-of-google-pagerank.html
PR(A) – Page Rank of page A
PR(Wi) – Page Rank of pages Wi which link to page A
C(Wi) – number of outbound links on page Wi
d – damping factor which can be set between 0 and 1.
PageRank is calculated as a recursive function, meaning the accuracy of a page’s ranks increases after every iteration. If we look at the following diagram below in figure 3.
Figure 3. PageRank Diagram: from http://codispatch.blogspot.com/2015/12/java-program-implement-google-page-rank-algorithm.html
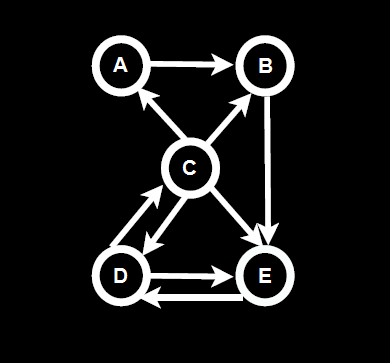
We can see the probabilistic distribution using eigenvector centrality. For example on the first or ‘zero’ iteration the PageRank value is calculated as an even distribution of 1 divided by N number of pages. Which would give a value of 0.2 for each of the 5 pages (1/n). As you can see in table 1 below.
Table 1: PageRank Values: from http://codispatch.blogspot.com/2015/12/java-program-implement-google-page-rank-algorithm.html
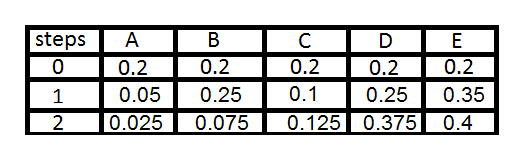 Once the initial zero iteration value has been calculated as seen in figure 4 above in the 0 row. The next iteration will then divide each page or node’s current rank by the number of outbound links. For example node C has 4 outgoing links so its initial value of 0.2 is divided by 4 to give a value of 0.05. As node A has 1 inbound link from node C it now has a value of 0.05. This process is repeated for all of the inbound and outbound links for each node and repeated for each iteration as show in the table in table 1.
Once the initial zero iteration value has been calculated as seen in figure 4 above in the 0 row. The next iteration will then divide each page or node’s current rank by the number of outbound links. For example node C has 4 outgoing links so its initial value of 0.2 is divided by 4 to give a value of 0.05. As node A has 1 inbound link from node C it now has a value of 0.05. This process is repeated for all of the inbound and outbound links for each node and repeated for each iteration as show in the table in table 1.
After this initial calculation has been made a dampening factor taking into account the probability of a user leaving the site is incurred. Note – Google employees have alluded to the fact that the dampening factor of the random surfer model lies somewhere between 0.7 and 0.85 (Levy, 2011).
POTENTIAL INTEGRATION INTO BRITIZEN
The concept of if eigenvector centrality utilised by Google’s PageRank algorithm can be applied successfully to the Britizen’s scoring system If the dampening factor induced by the random surfer model of the PageRank algorithm is discarded due to its irrelevance in peer to peer scoring. This is due to the fact that the hypertextual links are not hypothetically traversed as in Google’s model and are therefore superfluous in our design. Utilising the dispersal of scores via eigenvector centrality based on the peer to peer links on the site where a user’s number of friends represents even bidirectional links could induce certain desirable social behaviours. For example if a user had a small closely-nit group of friends with high Britizen points this would be more beneficial than having lots of friends with mediocre scores as the division of the users overall score would be dispersed equally to their peers. The implementation would of course only utilise eigenvector centrality as a weighted proportion or metric to calculate the user’s overall score, depending on how much social engineering is the focus of the scoring system. For more radical effects I believe a weighting of 50% of a user’s overall score would statistically show the greatest results as the user’s own background and whom they befriend would be calculated in equal measure, allowing us to observe the social effects of our scoring algorithm more clearly.
REFERENCES
Brin, S. & Page, L., 1998. The Anatomy of a Large-Scale Hypertextual Web Search Engine. Seventh International World-Wide Web Conference (WWW 1998), 14-18 April.
Chater, N. & Oaksford, M., 2008. The Probabilistic Mind: Prospects for Bayesian Cognitive Science. New York: Oxford University Press, USA.
Chitpady , S., 2017. Java Program to Implement Simple PageRank Algorithm. [Online]
Available at: http://codispatch.blogspot.com/2015/12/java-program-implement-google-page-rank-algorithm.html
[Accessed 23 April 2017].
Google, 2014. Our history in depth. [Online]
Available at: https://www.google.com/about/company/history
[Accessed 16 11 2016].
Levy, S., 2011. In The Plex: How Google Thinks, Works, and Shapes Our Lives. New York: Simon & Schuster.
Marchiori, M., 1997. The Quest for Correct Information on the Web: Hyper Search Engines. The Sixth International WWW Conference (WWW 97), 7-11 April.
Page, L., 2001. Method for Node Ranking in a Linked Database. USA, Patent No. US 6285999 B1.
Spertus, E., 1997. ParaSite: Mining Structural Information on the Web. The Sixth International WWW Conference (WWW 97), 7-11 April.
Webs, I., 2009. Simple Explanation of Google PageRank. [Online] Available at: http://interestingwebs.blogspot.co.uk/2009/05/simple-explain-of-google-pagerank.html

